今回はピタゴラスのお話。
ピタゴラスは紀元前5~6世紀の古代ギリシャで活躍した数学者であり哲学者でもある人。
画像引用元:Pythagoras – Wikipedia ピタゴラス(紀元前582年 – 紀元前496年)像
「ピタゴラスの定理(三平方の定理)」とは?
ピタゴラスは以下に示したような「ピタゴラスの定理(三平方の定理)」を発見した人として、特に理系の方はよくご存じかと思います。中学校の数学の教科書にも出てくるのかな。
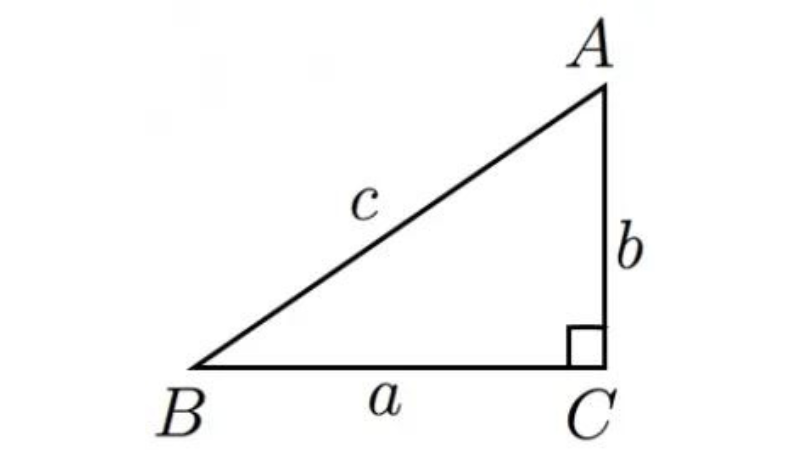
ピタゴラスの定理(三平方の定理):∠C=90∘ であるような直角三角形において,a2+b2=c2
引用元:三平方の定理の4通りの美しい証明 | 高校数学の美しい物語 (manabitimes.jp)
「ピタゴラスの定理」の証明方法はたくさん出されているようですが、参考までに一例を挙げておきます。
【ピタゴラスの定理の証明例】
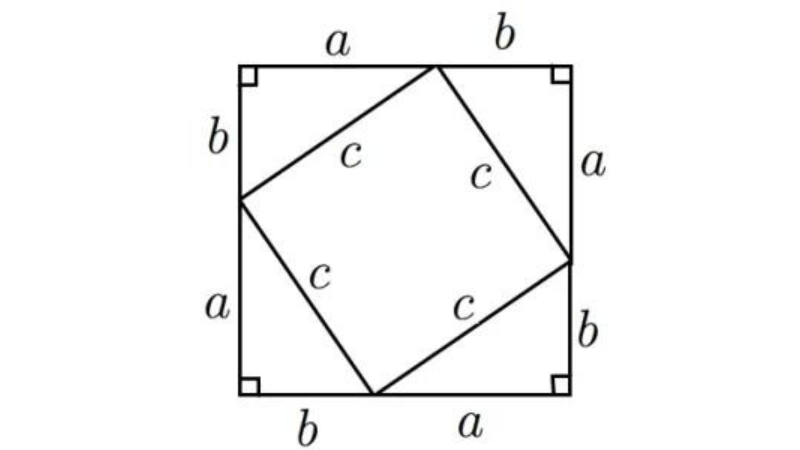
図において大きい正方形の面積 S を二通りで表す。
- 一辺(a+b)の正方形なので S=(a+b)2
- 一辺 c の正方形と直角三角形4つの和なので,S=c2+4×ab/2
よって,(a+b)2=c2+2ab
整理すると a2+b2=c2
となり三平方の定理を得る。
引用元:三平方の定理の4通りの美しい証明 | 高校数学の美しい物語 (manabitimes.jp)
「三平方の定理」以外のピタゴラスの大発見とは?
紀元前にこんな数学の発見をしていたこともすごいと思うのですが、ピタゴラスはなんと「音楽」の世界にも多大なる貢献をしているんですね。
音楽、特に音楽理論について詳しい方は既にご存じのことと思いますが、自分はピタゴラスが以下にお伝えする「音楽史上に残る大発見」をしたことを、誠に恥ずかしながらつい最近まで知りませんでした。
その「大発見」とは一言でいうなら、「二つの音の振動数の比が簡単で小さな整数で表せるとき、それらの音から作られる和音はよく調和する(心地よく聞こえる)」ということです。
これだけだとよく分からないと思いますので、もう少し具体的に見ていきましょう。
ピタゴラスは、ある日鍛冶屋の前を通りがかった時、複数のハンマーの音が作る重なり音(和音)を耳にしました。その時彼はその中に、きれいに調和して聞こえる音(協和音)と少し不安定に聞こえる音(不協和音)があることに気付きます。
彼はその原因を詳細に調べ、その後仲間とともに弦等を使って様々な実験をします。その結果ピタゴラスは次のことを発見しました。
出典:Pythagorean hammers – Wikipedia
- 振動数(周波数)が2倍の音は、高さは異なるが同じ音
- 振動数の比が2:3となる音の和音はよく調和する
(=基準音とその2分の3倍(=1.5倍)の振動数の音との和音はよく調和する)- 振動数の比が3:4となる音の和音はよく調和する
(=基準音とその3分の4倍の振動数の音との和音はよく調和する)- 振動数の比が8:9となる音の和音はあまり調和しない(不協和音)
振動数の「差」ではなく「比」が重要だということですね。
(ちなみに、上記ルール3はルール1と2から導けます。例えば、振動数が3の音の2倍音(振動数6の音)は基の音と同じ音なので、振動数6と振動数4の音は協和音となりルール2と同じことになります。)
「オクターブ」の誕生とピタゴラスが生んだ音律の弱点
次に、上記ルール1において、基準音(例えば「ド」の音)の2倍音は同じ音(1オクターブ上の「ド」)ですから、この基準音と2倍音の間の音を上記2のルールに基づいて決定していくことを考えます。
まず始めは、基準音(ここではわかりやすくするため「ド」の音を例に考えます)の3/2倍(=1.5倍)の振動数の音。
次は、それを更に1.5倍した音、になりますが、1.5×1.5=2.25は2倍音を超えることになるため、2を超えた場合は1/2倍して低い同じ音(振動数が2倍の音が同じ音ということは、高い音を基準に考えれば振動数が1/2倍の音も同じ音)にして、基準音と2倍音の間に収まる(基準音からの倍率が1~2の間になる)ようにします。つまり2.25/2=1.125倍音。
この操作を基準音から12回繰り返すと次のようになります。
| 基準音からの周波数倍率 | |
| ド(基準音) | 1 |
| ソ | 3/2=1.5 |
| レ | (3/2)2 x 1/2=1.125 |
| ラ | (3/2)3 x 1/2=27/16=1.6875 |
| ミ | (3/2)4 x (1/2)2=81/64=1.2656… |
| シ | (3/2)5 x (1/2)2=243/128=1.8984… |
| ファ# | (3/2)6 x (1/2)3=729/512=1.4238… |
| ド# | (3/2)7 x (1/2)4=2187/2048=1.0678… |
| ソ# | (3/2)8 x (1/2)4=6561/4096=1.6018… |
| レ# | (3/2)9 x (1/2)5=19683/16384=1.2013… |
| ラ# | (3/2)10 x (1/2)5=59049/32768=1.8020… |
| ミ# | (3/2)11 x (1/2)6=177147/131072=1.3515… |
| シ# | (3/2)12 x (1/2)6=531441/262144=2.0272… |
これを基準音からの倍率順(周波数順)に並べなおして、基準音の2倍音を加えると以下のようになります。
| 基準音からの周波数倍率 | |
| ド(基準音) | 1 |
| ド# | (3/2)7 x (1/2)4=2187/2048=1.0678… |
| レ | (3/2)2 x 1/2=1.125 |
| レ# | (3/2)9 x (1/2)5=19683/16384=1.2013… |
| ミ | (3/2)4 x (1/2)2=81/64=1.2656… |
| ミ# | (3/2)11 x (1/2)6=177147/131072=1.3515… |
| ファ# | (3/2)6 x (1/2)3=729/512=1.4238… |
| ソ | 3/2=1.5 |
| ソ# | (3/2)8 x (1/2)4=6561/4096=1.6018… |
| ラ | (3/2)3 x 1/2=27/16=1.6875 |
| ラ# | (3/2)10 x (1/2)5=59049/32768=1.8020… |
| シ | (3/2)5 x (1/2)2=243/128=1.8984… |
| ド(2倍音) | 2 |
| シ# | (3/2)12 x (1/2)6=531441/262144=2.0272… |
一番最後の「シ#」は殆ど「ド」に近い音になるのでこれで操作をやめます。
基準音の「ド」と2倍音の「ド」の間に11音、音の種類としては「ド」を入れて計12音の音階ができました。ピアノの鍵盤を見るとわかりますが、「ミ」の半音上が「ファ」、「シ」の半音上が「ド」になりますので、「ミ#」を「ファ」として長音階(メジャーコード)だけピックアップすれば「ドレミファソラシド」の完成です。(実際は2倍音の「ド」を2/3倍して「ファ」、それを更に2/3倍して2をかけて「シ♭」を作れるので周波数比はもう少し小さい数字で表すことができます。上記はあくまでも考え方を示しているとご理解願います。)
この「ドレミファソラシド」、基準の音「ド」から数えて八番目の音が元の音と同じになるため、これを「8度音程」、ラテン語では「8」を意味するoctを頭につけてoctavusといい、これがつまり「オクターブ」です。ちなみに8本足のタコは英語でoctopusといいますね。
そしてこのように上記ルール1、2から全ての音と音階を決める音律を「ピタゴラス音律」といいます。
この「ピタゴラス音律」はその後西洋音楽の基礎となります。そしてなんと初期ルネサンス(15世紀)まで西洋では標準的な音律となりました。すごいですね。
しかしながら、長く使われたこの「ピタゴラス音律」にも弱点がありました。
「ピタゴラス音律」で作られた音階は、周波数が2:3の関係の音(例えば「ド」と「ソ」)との調和は非常にいいのですが、例えば「ド」と「ミ」のような組み合わせの場合には(周波数比が上記81:64のようになり)小さな整数の比とならないため、調和があまりよくありません(物理的な理解としては唸りを生じてしまうことが考えられます)。
また、上記の最後の「シ#」は殆ど「ド」に近い音になるのですが、正確に基準音「ド」の2倍とはなりません。ほんの少しズレが生じます。このわずかのズレは「ピタゴラス・コンマ」と呼ばれ、そのズレの程度は半音の約1/4ですが、このズレのためにピタゴラス・コンマを跨いだときに不協和が発生してしまいます。
そこで「ド」と「ミ」のような組み合わせの場合にもきれいなハーモニーが得られるよう周波数比が小さい整数となるように修正したのが「純正律」というものです。「純正律」では例えば「ド」と「ミ」の周波数比が4:5となるような「ミ」の音を採用します。
しかしながら、これも音楽の進化とともに、移調(曲全体のキーを変える)や転調(曲の途中で調を変える)がしにくい等の問題が発生しました。
そこで現在一般的には「平均律」という音律が広く使用されています。これは1オクターブを均等な周波数比で12分割するというものです。即ち、基準音の周波数に12√2(2の12乗根。これを12回かけると2になる)をかけた周波数を持つ音を1つ上の音にするということです。
これは移調、転調がしやすく大変便利で、音の間隔が均等なため、どんな音を基準にしても音程が変わらないというメリットがあります。その一方、倍音以外の音とは周波数比が小さな整数にはならないため、きれいなハーモニーは出にくくなってしまいます。ですので、我々が普段耳にしている「平均律」で奏でられた音楽は少しハーモニーを犠牲にしているんですね。
ということで以上まとめますと、ピタゴラスが音を数学的(物理的)に解釈したことで「オクターブ」と「ドレミファソラシド」の音階が生まれ、その後音楽を理論的に解釈して発展させていくことが出来るようになりました。
このように無限にある様々な周波数の音の中で、よく調和する音を拾い上げて音階って作られているんですね。音楽にもこんな数学的なバックグラウンドがあるなんて知りませんでした。
それをピタゴラスはなんと紀元前にやっていたというのですから全く驚きです。
天才ってやっぱりすごいですね。